티스토리 뷰
[ML Andrew Ng] C1-Supervised Machine Learning: Regression and Classification 강의 (W1-2)
Life4AI 2024. 8. 20. 19:41
Linear Regression Model Part 1
회귀 모델은 지도학습의 한 종류로, 데이터 세트에 모든 정답이 나와있으며, 숫자를 결과로 예측한다.
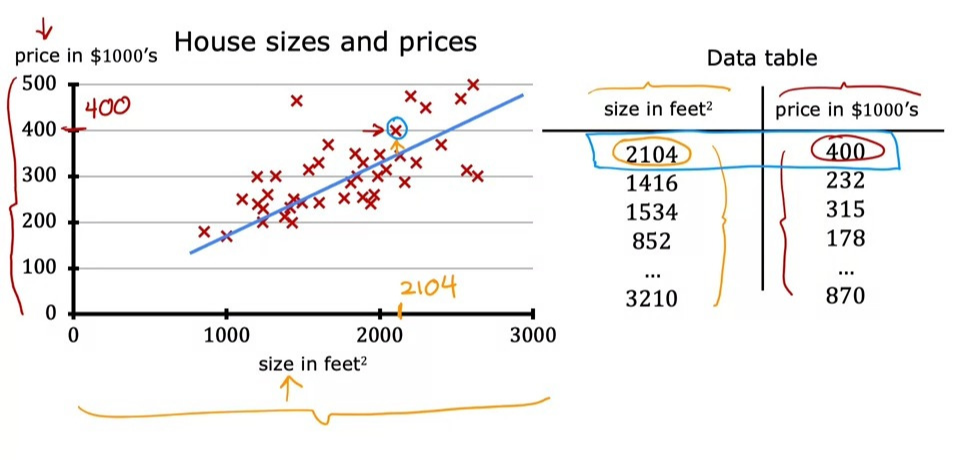
주택의 크기로 가격을 예측하는 모델이 회귀 모델의 한 예시이다.
여기서, 선형 회귀란 쉽게 데이터에 직선을 맞추는 것을 의미한다.
회귀 모델과 대조적으로, 분류 모델(classfication model)은 범주를 예측한다.

집 값 예측을 위한 training set을 가져온다고 할 때,
- \(x\) = 입력 값의 변수 (독립변수)
- \(y\) = 출력값의 변수 (종속변수)
- \(m\) = training examples의 총 개수
- \((x,y)\) = 하나의 training example
- \((x^{(i)},y^{(i)})\) = i번째 training example

Linear Regression Model Part 2
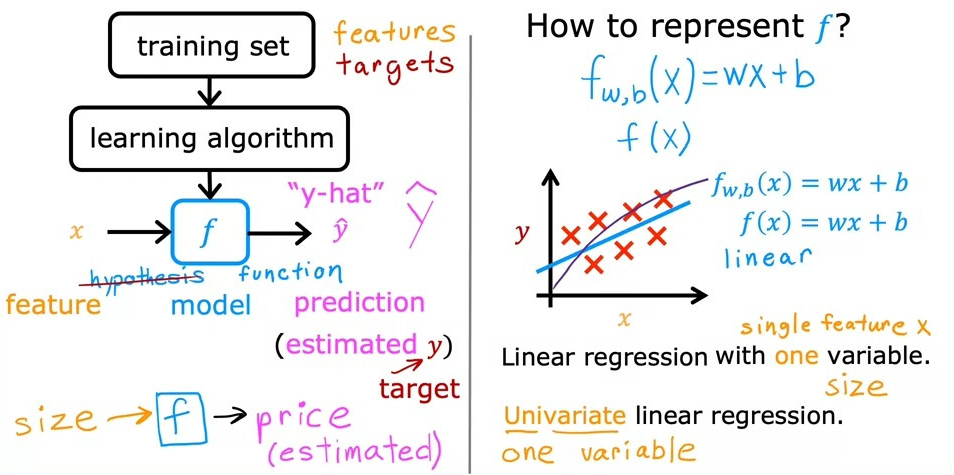
입력 특징(feature)과 출력 목표(label)를 모두 포함하는 훈련 세트를 학습 알고리즘에 공급하고, 지도학습 알고리즘이 함수 f를 생성해낸다. 이 함수를 우리는 model, hypothesis 라고 한다. (해당 강의에서는 그냥 함수 f라고 함)
그럼 함수 f는 새로운 입력 값 x로 예측값 y값(\(\hat{y}\))을 출력하고 추정하는 것이다.
그렇다면 모델 f를 나타내는 방법은???
\(f_{w,b}(x) = wx+b \) 이다.
해당 식은 일차함수(\(y=ax+b\))와 같은 꼴이라서, 이를 univariate linear regression이라고도 한다.
\(f_{w,b}(x)\)를 결정하는 변수가 하나뿐이기 때문이다.
Cost Function
Univariate linear regression에서 \(f_{w,b}(x)\)값을 예측하기 위한 모델을 다음과 같이 정의하였다.
여기서, \(w\)와 \(b\)를 parameter라고 한다.
이러한 parameter들의 값을 잘 찾아야 \(f_{w,b}(x)\)값을 잘 표현해 낼 수 있다.
그렇다면 각각의 \(w\)와 \(b\)는 어떻게 찾고, 정할까?

우선, \(w\)와 \(b\)가 어떤 역할을 하는지 살펴보자.
\(w\)와 \(b\)에 대해 선택한 값에 따라 x의 다른 함수 f가 생성되며, 이 함수는 그래프에 다른 선을 생성한다.
아래는 \(w\)와 \(b\)에 다양한 값을 넣었을 때 함수의 모양이 어떻게 변하는지 보여준다.

우리는 함수 f에서 얻은 직선이 기존 훈련 샘플들\((x^{(i)},y^{(i)}\))에 잘 맞도록 parameter \(w\)와 \(b\)의 값을 선택해야한다. 즉, \(f_{w,b}(x)\)의 값을 최대한 \(y\)와 비슷하거나 가까운 곳에 있도록 만들어야 한다.

따라서, \(f_{w,b}(x)\)와 \(y\)값이 최소가 되도록 \(w\)와 \(b\)의 값을 잘 찾아야한다.
함수 f의 선이 훈련 데이터에 얼마나 잘 맞는지 측정하는 방법은 비용함수를 생성하는 것이다.
비용함수는 \(\hat{y}\) 에서 y를 뺀 값인 오차(error)을 구하여, 예측값이 목표값으로부터 얼마나 멀리 떨어져있는지를 측정한다.
결국, 비용함수를 최소화하는 \(w\)와 \(b\)를 찾고자하는 것이 목표이다.
다시말하면, \(\hat{y}\)와 \(y\)값의 편차를 최소한으로 줄여서 \(w\)와 \(b\)의 값을 최소화해야 한다.

제곱 오차(squared error)을 사용하는 데, 훈련 세트의 크기가 커져도 커지지 않는 비용함수를 만들기 위해 총 제곱 오차 대신 평균 제곱 오차를 계산하기 위해 m으로 나누었다. (m = training examples의 개수)
그리고, 1/2로 나누는 이유는 gradient descent를 활용하여 편미분을 하였을 때, 제곱이 내려와 1/2를 상쇄하기 때문이다.
Cost Function Intuition
왼쪽은 지금까지 비용함수에 대해 살펴본 내용이고, 오른쪽은 편의를 위해 상수항을 제거한 단순화된 버전이다. 그러면, x가 0이면 y도 0이므로 원점을 지나간다. (y=ax)

우리의 목표는 \(w\)와 \(b\)의 cost function을 최소화해야하는 데, \(b\)가 없어졌으니 \(w\)의 cost function만 최소화하면 된다.

예를 들어, \(w\)가 1이라고 가정해보자. 빨간색의 X가 데이터들이라고 하자.
이때의 비용 J를 계산하면, \(\hat{y}\)와 \(y\)값들이 모두 일치하므로 그 편차가 0이 되므로, 최종적인 J은 0이 될 것이다. 오른쪽 \(w\)와 \(J(w)\)에 대한 그래프를 그리면, \(w\)가 1일 때, \(J(w)\) 값은 0이 될거라 해당 위치에 도표화하겠다.

이번에는 \(w\)가 0.5이라고 해보자. 이때의 비용 J를 계산하면, \(\hat{y}\)와 \(y\)값들이 다르며, 위와 같이 계산하면 최종적인 J은 0.58이 될 것이다. 오른쪽 \(w\)와 \(J(w)\)에 대한 그래프를 그리면, \(w\)가 0.5일 때, \(J(w)\) 값은 0.58이 될거라 해당 위치에 도표화하겠다.

이렇게 계속 다양한 \(w\)값들을 대입하면, 오른쪽과 같이 이차함수를 얻을 수 있다.

우리의 목표는 \(J(w)\)을 최소화하는 것이었기 때문에, \(w\)의 값이 1일 때 \(J(w)\)의 최소값인 것을 쉽게 알 수 있다.
Visualizing the Cost Function

이제는 \(w\)와 \(b\)을 동시에 조정해보자. 여기서는, 앞서 우리가 봤던 변수가 하나뿐 \(w\)이었던거와 달리 변수가 2개(\(w\)와 \(b\))이다.
\(J(w, b)\)의 개형은 2개의 독립변수 \((w, b)\)와 하나의 종속변수(\(J(w, b)\))로 이루어져있기 때문에 3차원 그래프의 개형이 나타날 것이다. 그 개형은 아래와 같다.

이 3차원 그래프에서 우리는 J값이 가장 낮은 지점(파란색 부분)을 구해야한다.

등고선이 같다면 \(w\)와 \(b\)값이 달라도, 같은 비용 함수 \(J\)을 가지며, 우리는 \(w\)와 \(b\)값을 조정해서 비용함수 J가 최대한 타원의 중심에 오도록 해야한다.

예를 들어, \(w\)는 음의 0.15와 같고 \(b\)는 800일 때, 비용 J는 오른쪽에 보이는 곳에 표시된다. 함수 f가 데이터에 잘 맞지 않다는 것을 볼 수 있다. 이는 적합하지 않기 때문에 J의 그래프를 보면, 이 선의 비용이 최솟값과 거리가 먼 것을 볼 수 있다.

이번에는 \(w\)는0이고 \(b\)는 360일 때, 비용 J는 오른쪽에 보이는 곳에 표시된다.

이번에는 \(w\)는 약 음의 0.15와 같고 \(b\)는 500일 때, 비용 J는 오른쪽에 보이는 곳에 표시된다.

마지막 예제를 보면, f가 이제 훈련 세트에 꽤 잘 맞습니다. 오른쪽에서 볼 수 있듯이 비용을 나타내는 점이 타원의 중심에 매우 가깝다.
Practice quiz: Regression

'AI > Machine learning' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 강화학습
- ML와 DL 차이
- CNN에서의 활성화 함수
- 앤드류응
- 머신러닝
- 숏코딩
- NumPy
- Sort
- ML 프로세스
- Andrew Ng
- 파이썬
- **
- 로지스틱 회귀
- **kwargs
- 경사하강법
- baekjoon
- ML 학습 방법
- python
- 강의노트 정리
- 머신러닝 프로세스
- 손실함수
- 딥러닝
- 비용함수
- droput
- ML
- cnn
- *
- 백준
- *args
- sorted
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
