티스토리 뷰
[ML Andrew Ng] C1-Supervised Machine Learning: Regression and Classification 강의 (W3-2) Classification
Life4AI 2024. 9. 9. 15:49
Cost Function - Cost Function for Logistic Regression
비용 함수(cost function)는 특정 파라미터 집합이 훈련 데이터에 얼마나 잘 맞는지 측정하는 방법을 제공한다. 따라서 더 나은 파라미터를 선택할 수 있습니다.
이제, 제곱 오차 비용 함수(squared error cost)가 로지스틱 회귀 분석에 적합하지 않은 이유와 로지스틱 회귀에 더 적합한 비용 함수에 대해 알아보겠다.
로지스틱 회귀 모델을 위한 훈련 세트는 다음과 같다.

이는 이진 분류 작업이므로 대상 레이블 \(y\) 0 또는 1 값을 가진다.
주어진 훈련 세트를 사용하여, 우리는 어떻게 파라미터 \(w\)와 \(b\)를 선택할지 고민한다.
선형 회귀에서는 제곱 오차 비용 함수가 널리 사용된다. 이 함수는 볼록한 형태를 가지며, 이는 그릇 모양으로 생겨서 경사 하강법을 통해 쉽게 전역 최소값에 도달할 수 있다.

그러나 제곱 오차 비용 함수를 로지스틱 회귀에 적용할 경우, 이 함수는 더 이상 볼록하지 않다.
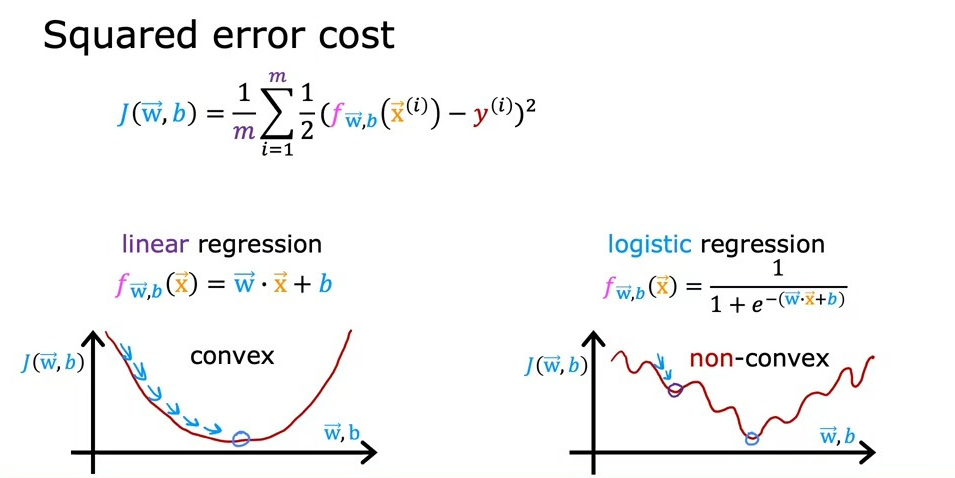
볼록하지 않은 함수는 여러 지역 최소값이 존재할 수 있으며, 경사 하강법이 이러한 점들에 빠질 가능성이 있다. 따라서 로지스틱 회귀에서는 제곱 오차 비용 함수가 적합하지 않다.
따라서, 로지스틱 회귀에 적합한 비용 함수를 정의해야한다.
이때, 각 훈련 데이터에 대한 손실함수를 정의한다. (\(L(f_{\vec{w},b}(\vec{x}^{(i)}, y^{(i)}) = (f_{\vec{w},b}(\vec{x}^{(i)} - y^{(i)}))^{2} \))

이 손실함수는 실제 레이블 \(y\)가 1일 때와 0일 때각각 다르게 계산된다.
1. \(y=1\)인 경우

\(y=1\)일 때 손실 함수는 로그 함수의 형태를 가진다.
이때, 예측값 \(f(x)\)가 1에 가까울수록 손실은 거의 0에 가까워지며, 예측이 정확할수록 손실이 작아진다. 반대로, \(f(x)\)가 0.1처럼 작은 값일 때는 손실이 크게 증가한다.
즉, 모델이 실제 레이블이 1인 경우에는 더 정확하게 1에 가까운 값을 예측하도록 장려된다.
2. \(y=0\)인 경우
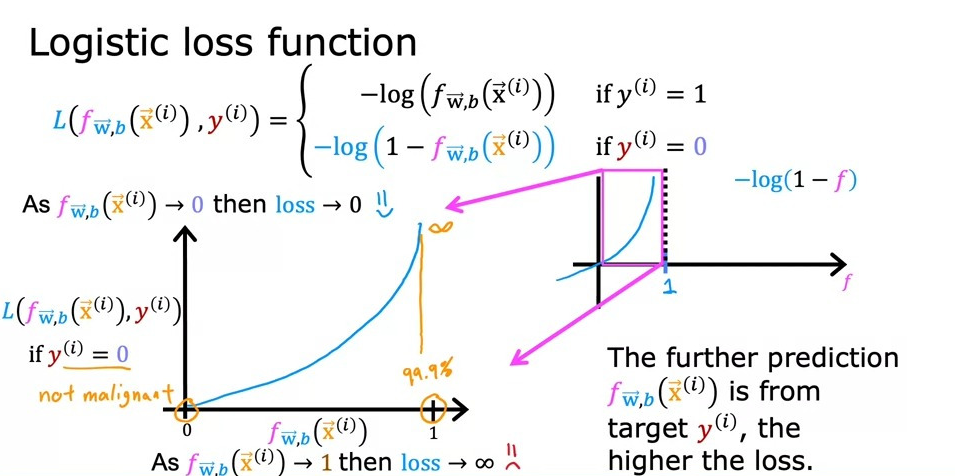
\(y=0\)일 때 손실 함수는 \(1-f(x)\)로 정의된다.
이때, 예측값 \(f(x)\)가 0에 가까울수록 손실은 작아진다. 만약 모델이 1에 가까운 값을 예측한다면, 실제 레이블과 멀어졌기 때문에 손실은 크게 증가한다. 예를 들어, 종양이 악성이 아니라고 실제로 판명되었는데 모델이 악성일 확률이 99.9%라고 예측했다면, 모델은 큰 손실을 얻게 된다.
로지스틱 회귀의 손실 함수는 훈련 세트의 모든 예제에서 발생한 손실을 합산하여 비용 함수를 만든다. 이 비용 함수는 볼록 함수로, 경사 하강법을 안정적으로 적용할 수 있어 전체 최소값을 찾는 데 유리하다.

비용 함수는 개별 훈련 예제에서 발생한 손실의 평균을 구하고, 그 값을 최소화하는 파라미터 \(w\)와 \(b\)를 찾는 것이 목표이다. 이를 통해 로지스틱 회귀 모델이 데이터에 가장 잘 맞는 파라미터를 얻게 되는 것이다.
Cost Function - Simplified Cost Function
로지스틱 회귀에서 손실 함수와 비용 함수를 더욱 간단하게 표현하는 방법을 소개하겠다. 이를 통해 모델의 파라미터를 더 쉽게 최적화할 수 있다.(경사하강법 구현이 더 간단해질 수 있음)
로지스틱 회귀의 손실 함수는 \(y\)가 0 또는 1의 값만 가지기 때문에 두 경우를 따로 정의할 필요 없이 하나의 통합된 식으로 표현할 수 있다. 이렇게 하면 수식이 간단해지고 계산도 더 효율적이다. 이를 통해 모델을 더 쉽게 이해하고 구현할 수 있다.

이 수식에서
- \(y=1\)인 경우: 손실은 \( -log(f(x)) \)로, 예측값 \(f(x)\)가 1에 가까울수록 손실이 줄어든다.
- \(y=0\)인 경우: 손실은 \( -log(1-f(x)) \)로, 예측값 \(f(x)\)가 0에 가까울수록 손실이 줄어든다.

위처럼 두 경우를 하나의 수식으로 통합하면, \(y\)가 1이든 0이든 동일한 방식으로 계산할 수 있다.
단순화된 손실 함수를 사용하여 로지스틱 회귀에 대한 비용 함수를 작성해 보겠다.

이 비용 함수는 볼록 함수이기 때문에 경사 하강법을 통해 전역 최솟값에 도달할 수 있습니다. 즉, 비용 함수의 최솟값을 찾으면 모델의 최적 파라미터 \(w\), \(b\)를 찾을 수 있다.
로지스틱 회귀에서 사용되는 이 비용 함수는 최대우도 추정(Maximum Likelihood Estimation, MLE)이라는 통계적 방법에서 유도되었다. MLE는 주어진 데이터에 대해 모델이 가장 잘 맞는 파라미터를 찾는 방법으로, 로지스틱 회귀의 비용 함수는 이 원리를 따른다.
Practice quiz : Cost function for logistic regression

'Coursera 강의 > Machine learning Specialization' 카테고리의 다른 글
- Total
- Today
- Yesterday
- baekjoon
- 비용함수
- policy function
- 백준
- sorted
- 11870
- state value function
- 손실함수
- 숏코딩
- action value function
- Andrew Ng
- 경사하강법
- NumPy
- 강화학습
- python
- 강의노트 정리
- omp: error #15
- numpy 배열 생성
- 딥러닝
- 파이썬
- adrew ng 머신러닝 강의
- **kwargs
- **
- Sort
- numpy 배열 속성
- 앤드류응
- computation graph
- 로지스틱 회귀
- *args
- *
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
