티스토리 뷰
[ML Andrew Ng] C1-Supervised Machine Learning: Regression and Classification 강의 (W1-3)
Life4AI 2024. 8. 27. 16:54
Gradient Descent
경사하강법(gradient descent)에 대해 공부해보자.

Gradient descent를 직역하면 'gradient(기울기)를 타고 내려온다' 정도로 해석할 수 있겠는데,
이는 마치 3차원 그래프상에서 임의의 시작점 (\(w,b)\)에서 출발하여 가장 가파르게 경사진 방향으로 내려가 최소값(minimum)에 도달하는 과정이다.

위의 그림을 보면, 시작점에 따라 다른 지점에서 종료되는 것을 알 수 있다.
오른쪽 지점은 local minimum으로, 극솟값에 해당한다. 그러나, 우리가 찾고자 하는 것은 진정한 최소값(global minimum)이므로, local mimimum에 빠지지 않도록 주의해야 한다. 이를 피하기 위한 방법도 추후에 배우게 될 것이다.
Gradient descent의 알고리즘은 아래와 같은 방식으로 동작한다.

1. 기존 \(w\)값에서 비용함수 \(J(w, b)\)를 \(w\)에 대해 편미분한 값에 학습률 \(\alpha\)를 곱한 값을 빼준다.
2. 동시에, 기존 \(b\) 값에서도 비용함수 \(J(w, b)\)를 \(b\)에 대해 편미분한 값에 학습률 \(\alpha\)값을 곱한 값을 빼준다.
중요한 점은, \(w\)와 \(b\)의 업데이트가 동시에 이루어져야 한다는 것이다. 즉, 코드 작성 시 왼쪽과 같이 \(w\)와 \(b\)를 동시에 조정해야한다. 만약 오른쪽과 같이 작성하면, \(w\)을 조정한 후 변화된 \(J(w, b)\) 값을 바탕으로 \(b\)를 조정하게 되어, 두 변수의 업데이트가 정확하게 이루어지지 않는다. 따라서, 경사하강법의 성능을 보장하기 위해서는 반드시 \(w\)와 \(b\)를 동시에 업데이트하는 방식으로 구현해야 한다.
Gradient Descent Intuition
앞서 살펴본 Gradient Descent 알고리즘을 더 쉽게 이해하기 위해, 이제 학습률과 도함수가 어떻게 작동하는지 직관적으로 알아보자.

이를 위해 매개변수 하나만 사용하는 간단한 예시를 들어보겠다.
여기서는 \(w\)라는 하나의 매개변수를 사용해 비용 함수 \(J(w)\)를 최소화하려고 한다. 이때 학습률 \(\alpha\)는 항상 양수로 설정된다.

만약 \(J(w)\)의 값이 양수라면,
앞의 뺄셈 기호로 인하여 \(w\)의 값은 줄어들어 왼쪽으로 이동할 것이다.

만약 \(J(w)\)의 값이 음수라면,
앞의 뺄셈 기호로 인하여 \(w\)의 값이 증가하여 오른쪽으로 이동할 것이다.
>>> 이러한 과정이 반복되면서 결국 \(w\)는 local minimum에 도달하게 된다.
Learning Rate
그렇다면 학습률 \(\alpha\)은 어떻게 설정해야 할까?

학습률 \(\alpha\)는 우리가 한번에 얼마나 크게 경사하강을 할지 결정한다.
예를 들어, 만약 \(\alpha\)가 너무 작다면, gradient descent는 매우 느리게 진행되어 수렴하는 데 오랜시간이 걸릴 것이다. 반대로, \(\alpha\)가 너무 크다면, gradient descent는 minimum을 지나버려 오히려 overshoot(초과 이동)할 가능성이 높아진다.
그러므로 최적의 \(\alpha\)를 정하는 것이 매우 중요하다.

한번 설정한 학습률 \(\alpha\)는 일반적으로 학습 과정에서 변경할 필요는 없다.
왜냐하면, gradient descent 알고리즘의 특성상 비용함수 \(J\)의 기울기(도함수) 값이 점점 0에 가까워질수록, 학습률 \(\alpha\)를 곱한 값도 자연스럽게 작아지기 때문이다.
이 과정을 자세히 보면:
1. 초기에는 비용 함수 \(J(w)\)의 기울기가 크기 때문에, 경사하강법이 큰 폭으로 진행된다. 즉, \(w\)의 값이 크게 조정된다.
2. 시간이 지나면서, \(w\)값이 점점 최소값에 가까워질수록, 기울기(도함수)값이 점점 작아진다.
3. 기울기가 작아지면, \(w\)의 변화량도 줄어들게 된다. 즉, 경사하강법의 속도가 느려지면서 \(w\)가 천천히 최소값에 접근하게 된다.
이렇게 기울기가 작아지면서 서서히 최소값에 도달하게 되므로, \(\alpha\)를 한번 설정한 후에는 굳이 변경할 필요가 없다. 너무 큰 변화를 피하면서 점진적으로 최소값을 찾아가는 과정이 자연스럽게 이루어지게 된다.
Gradient Descent for Linear Regression

gradient descent의 편미분값을 구한다고 했는데, \(J(w,b)\)를 \(w\), \(b\)로 편미분한 값은 각각 다음과 같다.

따라서, 경사하강법 알고리즘은 아래와 같으며, 수렴할때까지 w와 b를 반복적으로 업데이트한다.
그리고 반드시 w와 b는 동시에 업데이트해야한다는 것을 잊으면 안된다.

Linear Regression에서 비용 함수 \(J(w, b)\)를 구할 때, 항상 항아리 모양의 3차원 그래프가 나오게 된다. 이 그래프는 아래로 볼록한 모양을 하고 있으며, 이 모양은 수학적으로 "Convex Function"(볼록 함수)이라고 부른다.
Convex Function의 중요한 특징은, 그래프가 오직 하나의 global optimum을 가진다는 점이다. 이는 우리가 Gradient Descent를 사용하여 이 함수를 최적화할 때, 시작 지점에 상관없이 결국에는 이 최솟값에 도달하게 된다는 것을 의미한다.
다시 말해, 비용 함수 \(J(w, b)\)는 하나의 글로벌 최솟값을 가지기 때문에, 경사하강법이 잘 작동하며, 이 최솟값을 찾아내어 최적의 \(w\)와 \(b\)값을 구할 수 있게 된다.
Running Gradient Descent



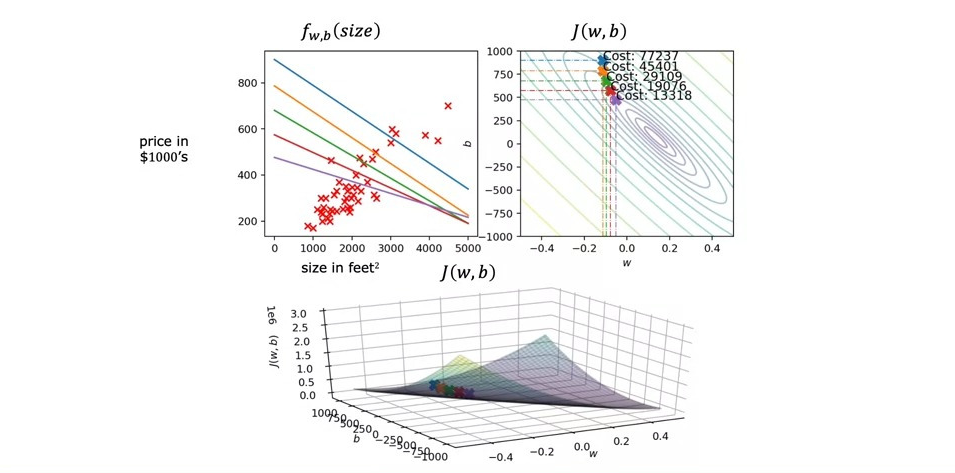

위의 슬라이드들은 gradient descent로 인해 \(w\)와 \(b\)의 값의 변화가 어떻게 univariate linear regression에 영향을 주는지 보여준다.

우리가 배운 경사하강법은 "Batch Gradient Descent"라고도 불린다. 그 이유는 경사하강법을 한 번 적용할 때, 모든 훈련 데이터(training examples)를 사용해서 비용 함수의 기울기를 계산하기 때문이다.
다시 말해, 각각의 데이터 포인트에서 발생하는 오차를 모두 더한 후에 그 합을 이용해 매개변수들을 업데이트하는 방식이기 때문에 "Batch"라는 이름이 붙은 것이다.
Practice quiz: Train the model with gradient descent

'AI > Machine learning' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 강화학습
- sorted
- baekjoon
- 손실함수
- Sort
- NumPy
- 게리맨더링2
- **
- *args
- ai 필요성
- counter()
- pytohn
- 비용함수
- python
- 앤드류응
- ai 필요?
- ai 중요한 이유
- 경사하강법
- ai란?
- 강의노트 정리
- Andrew Ng
- 데이터 얼마나 수집
- 데이터 충분?
- 파이썬
- 숏코딩
- **kwargs
- *
- 백준
- 로지스틱 회귀
- 딥러닝
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |

