티스토리 뷰
[ML Andrew Ng] C1-Supervised Machine Learning: Regression and Classification 강의 (W2-1) Linear Regression with Multiple Variables
Life4AI 2024. 9. 5. 12:17
Linear Regression with Mulitple Variables - Mutiple Features
다중 선형 회귀(Multiple linear regression)에 대해서 공부해보자.

Univariate linear regression과 달리, multiple feature은 종속 변수 y를 결정하는독립변수(feature)가 여러 개이다. 이를 간단하게 표현하면,
- \(n\) = feature(독립 변수)의 개수
- \(x^{(i)}\) = \(i\)번째 training example의 모든 features
- \(x_{j}^{(i)}\) = \(i\)번째 training example의 \(j\)번째 feature
임을 뜻한다.

Univariate linear regression의 가설과는 달리, multiple feature이 있을 경우에는 가설을 이러한 여러 feature 에 맞게 설정하고, 각각의 parameter을 조정한다. (위 슬라이드는 feature이 4개)

parameter \(w\)와 input \(x\)를 vectorized form으로 구성한 다음, 이 둘을 dot product(내적)하면, 간결한 형태로 모델을 표현할 수 있다.
이처럼 여러 입력 특성을 가진 선형 회귀 모델을 multiple linear regression(다중 선형 회귀)이라고 부른다.
Linear Regression with Mulitple Variables - Vectorization Part I

NumPy dot 함수는 두 벡터 사이의 점 곱 연산을 벡터화하여 구현한 것으로, 특히 \(n\)이 클 경우 이전 두 코드 예제보다 훨씬 빠르게 실행된다. (NumPy dot 함수가 병렬 하드웨어를 사용할 수 있기 때문에 앞서 살펴본 for 루프나 순차 계산보다 훨씬 효율적이다)
벡터화를 하면, 코드가 더 짧아지므로 작성하기 쉽고, 실행속도도 훨씬 빨라지는 장점이 있다.
Linear Regression with Mulitple Variables - Vectorization Part II
벡터화된 구현이 백그라운드에서 어떻게 작동하는 지 살펴보자.

벡터화를 사용하지 않고 for 루프를 사용할 경우, j의 범위가 0에서 15라면 각 연산이 순차적으로 수행된다.
반면, Numpy의 벡터화된 함수는 벡터 \(w\)와 \(x\)의 모든 값을 한번에 계산한다. 즉, \(w\)와 \(x\)의 각 요소를 병렬로 곱한 후, 그 결과를 매우 효율적으로 더한다. 이 과정에서, 별개의 덧셈을 하나씩 수행할 필요없이 16개의 값을 동시에 처리한다.
즉, 벡터화를 적용하면 계산이 훨씬 빠르게 이루어진다. 이는 특히 대규모 데이터 세트를 학습할 때 더 중요하며, 이는 기계 학습의 경우가 많다. (벡터화를 통해 학습 알고리즘을 효율적으로 실행하여 현재 많은 최신 기계 학습 알고리즘의 대규모 데이터 세트로 잘 확장되는 핵심 단계였던 이유)
이제 다중 선형 회귀를 구현에서 벡터화가 어떻게 활용되는 지 구체적으로 살펴보자. 16개의 매개변수 w를 업데이트한다고 가정하자.

벡터화를 사용하지 않으면, for 루프를 통해 16번의 계산을 순차적으로 수행해야 한다.
하지만, 벡터화를 적용하면, 16개 값을 병렬로 처리한다. 벡터 \(w\)에서 16개의 값을 모두 한번에 빼고, 벡터 \(d\)에 있는 16개의 값을 0.1배 한 후, 이를 한번에 \(w\)에 반영한다.
결과적으로, 벡터화를 사용하면 선형 회귀 모델을 훨씬 더 빠르고 효율적으로 구현할 수 있다.
Linear Regression with Mulitple Variables - Gradient Descent for Mulriple Regression

매개변수 \(W\)를 \(w_{1}\)부터 \(w_{n}\)까지 열거하는 데신 \(W\)라고 간편화할 것이다.
model, cost function, gradient descent은 위 슬라이드와 같은 형태로 표현될 것이다.
더 깊이 들어가기 전에, 다중 선형 회귀에서 gradient descent 특히 도함수 항에 대해 더 자세하게 비교하자.
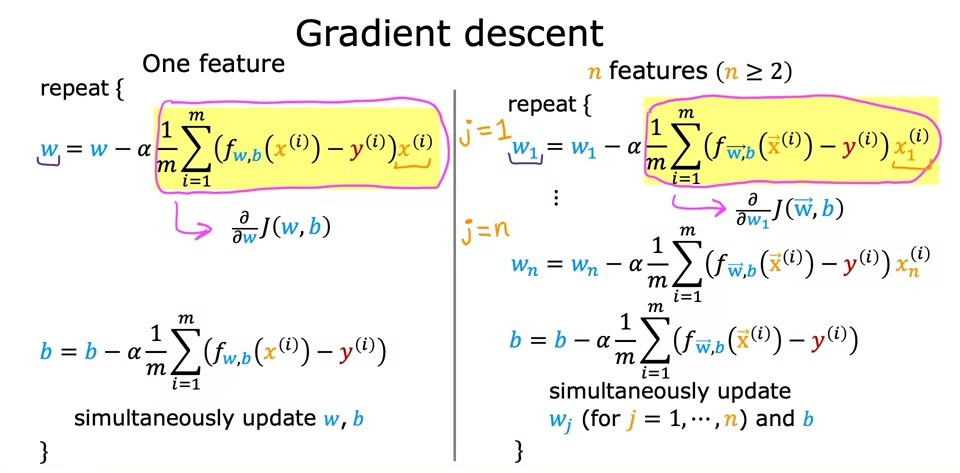
하나의 특징에 비해 여러 특징이 있을 때 약간 달라지는 것을 볼 수 있다.
결과적으로, 다중 선형 회귀에서 gradient descent를 사용할 때, 각 \(w_{n}\)값을 편미분하고, 이를 특정 학습률(learning rate)과 곱한 후, 모든 \(w\)값을 동시에 업데이트한다. 이렇게 하면 각 매개변수가 동시에 조정되면서, 최적의 값을 찾아가는 과정을 빠르게 수행할 수 있다.
Practice quiz: Multiple linear regression


'Coursera 강의 > Machine learning Specialization' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 경사하강법
- *args
- 강의노트 정리
- 비용함수
- 강화학습
- 숏코딩
- omp: error #15
- sorted
- action value function
- 앤드류응
- numpy 배열 생성
- **kwargs
- adrew ng 머신러닝 강의
- Sort
- state value function
- baekjoon
- 딥러닝
- 백준
- policy function
- Andrew Ng
- 손실함수
- numpy 배열 속성
- python
- **
- NumPy
- computation graph
- 로지스틱 회귀
- 파이썬
- *
- 11870
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
