티스토리 뷰
Coursera 강의/Deep Learning Specialization
[DL 딥러닝] Andrew Ng - Neural Networks and Deep Learning 강의 (1-2 신경망과 로지스틱 회귀)(4) 로지스틱 회귀 경사하강법
Life4AI 2024. 8. 14. 15:43로지스틱 회귀의 경사하강법에 대해서 알아보자

로지스틱 회귀의 경사하강법 - 단일 훈련 샘플
다음은 로지스틱 회귀이다.

- a : 로지스틱 회귀의 출력 값
- y : 실제 값
- \( L(a,y) \) : 하나의 샘플에 대한 손실 함수
아래는 로지스틱 회귀를 계산 그래프로 나타낸 것이다.
이 예제는 특성이 \(x_{1}\)과 \(x_{2}\) 2개이다.

여기서 구하고자 하는 것은 이 손실 함수의 도함수이다.
역방향으로 가서, \(da\), \(dz\), \(dw_{1}\), \(dw_{2}\), \(db\)를 구해보자.
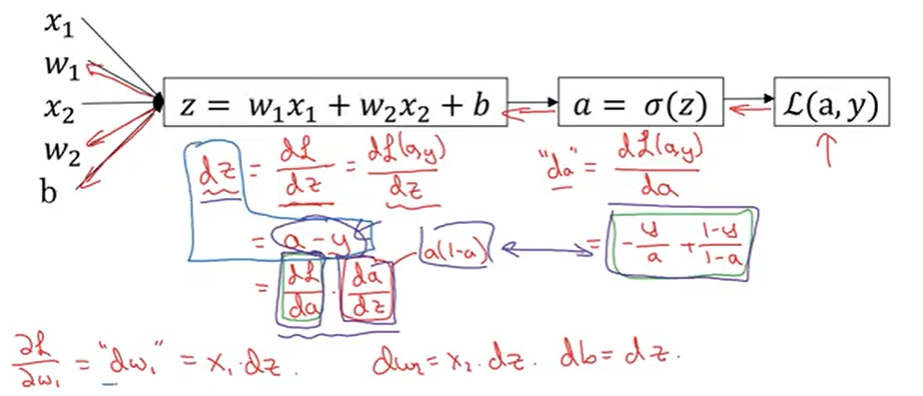
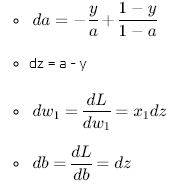
이렇게 계산하고 나면, 다음과 같이 갱신한다.

도함수를 계산하고, 단일 샘플에 대한 로지스틱 회귀의 경사하강법을 구현하는 방법을 알아보았다.
하지만, 로지스틱 회귀 모델을 훈련시키려면 단일 샘플이 아니라 m개의 훈련 샘플을 가진 훈련세트 전체를 훈련해야한다.
이제 알아보자.
로지스틱 회귀의 경사하강법 - m개의 훈련 샘플
m개의 훈련 샘플을 훈련 시킨 모델의 비용함수는 다음과 같다.
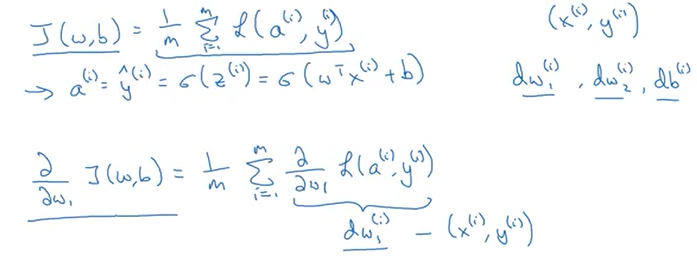
이를 코드로 표현하면 아래와 같다.

현재 코드에서는 특성의 개수를 2개로 가정하였지만, 만약 특성의 개수가 많아진다면 이 또한 for문을 이용해 처리해야 한. 즉, 이중 for문을 사용하게 되며 이로인해 계산속도가 느려지게 된다.
다음에는 vectorization을 통해 for문을 사용하지 않고 처리할 수 있는 방법을 배울거다.
'Coursera 강의 > Deep Learning Specialization' 카테고리의 다른 글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- *args
- 비용함수
- 백준
- Sort
- 로지스틱 회귀
- omp: error #15
- state value function
- 11870
- NumPy
- 앤드류응
- adrew ng 머신러닝 강의
- **kwargs
- action value function
- numpy 배열 생성
- baekjoon
- 경사하강법
- python
- numpy 배열 속성
- 강의노트 정리
- 강화학습
- 파이썬
- **
- *
- sorted
- 딥러닝
- policy function
- 손실함수
- Andrew Ng
- 숏코딩
- computation graph
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
글 보관함
