티스토리 뷰
[DL 딥러닝] Andrew Ng - Neural Networks and Deep Learning 강의 (1-2 신경망과 로지스틱 회귀) (1) 이진분류, 로지스틱 회귀
Life4AI 2024. 8. 12. 19:02신경망에서 학습하는 방법은 정방향 전파와 역전파가 있다. 로지스틱 분류로 신경망이 왜 전방향 전파와 역전파로 구성되어 있는지 직관을 얻어보자.

이진 분류 (Binary Classification)
이진 분류란 그렇다와 아니다 2가지로 분류하는 것이다. 이때 결과가 "그렇다" 이면 1로 표현하고 "아니다"이면 0으로 표현한다.
ex) 고양이다 (1) / 고양이가 아니다 (0).

- \(x\) : 입력 특성
- \(y\) : 주어진 입력 특성 \(x\) 에 해당하는 실제 값
- \( (x,y) \) : 한쌍의 훈련 샘플
- \(m\) : 훈련 샘플의 갯수
- \( n_{x} \) : \(x\)에 대한 차원
신경망을 구현할 때, 여러 훈련 샘플에 관한 데이터를 각각의 열로 놓는 것이 유용하다.
로지스틱 회귀 (Logistic regression)
로지스틱 회귀란 답이 0 또는 1로 정해져 있는 이진 분류 문제에 사용되는 알고리즘이다.

입력값 \(x\)와 파라미터 \(w\), \(b\)를 주어주고 예측값 \( \hat{y} \)을 얻게 된다.
- \(x\) : 입력 특성
- \(y\) : 주어진 입력 특성 \(x\) 에 해당하는 실제 값
- \( \hat{y} \) : \(y\)의 예측값 (0 ≤ \(\hat{y}\) ≤ 1 )
- 파라미터
- \(w\) : \(n_x\) 차원 상의 벡터
- \(b\) : 실수
\(\hat{y}\) 은 어떻게 출력할까?
선형회귀는 \( y=W^{T}X + b \) 로 계산하지만, 해당 값은 0과 1을 벗어날 수 있다. ( \(y\) 의 예측값은 \(y\) 가 1일 확률이기 때문에 항상 0과 1사이여야 한다.)
따라서, Sigmoid 함수를 적용해야 출력값을 0과 1사이의 값으로 변환해준다.
로지스틱 회귀를 위한 \( y = \sigma W^{T}X + b \)로 구한다.
참고)


여기서, \(z\)는 \( W^{T}X+b \)이다.
\(z\)가 실수일 때, \(z\)의 sigmoid는 \(sigma(z)=1/(1+e^{-z}) \)이다.
- \(z\)가 아주 크면, \(e^{-z}\)가 0으로 수렴한다. -> z의 sigmoid가 1으로 수렴한다.
- \(z\)가 아주 작으면, \(e^{-z}\)가 엄청 큰 수로 수렴한다. -> z의 sigmoid가 0으로 수렴한다.
로지스틱 회귀를 구현할 때, y가 1일 확률을 잘 예측하기 위해 매개변수 w와 b를 학습해야 한다.
로지스틱 회귀 (Logistic regression)의 비용함수(Cost function)
매개변수들 w와 b를 학습하려면 비용함수를 정의해야한다.

\(\hat{y}\)는 w의 \( W^{T}X+b \)의 sigmoid이다.
로지스틱 회귀 모델의 매개변수들 w와 b를 주어진 m개의 훈련 샘플로 학습할 때,
당연히 훈련세트를 바탕으로 출력한 \(\hat{y}^{(i)}\)값이 훈련세트에 포함된 실제값 \(y^{(i)}\)에 가까워지도록 하고 싶을 것이다.
즉, 우리의 목표는 실제값(\(y)\)에 가까운 예측값(\(\hat{y})\)을 구하는 것이다.
그럼 알고리즘이 잘 가동되는 지 어떻게 알 수 있을 까?
손실 함수(Loss function) 또는 오차 함수(Cost function)로 알 수 있다.
손실함수는 하나의 입력 특성(x)에 대한 실제값(\(y)\)과 예측값(\(\hat{y})\)의 오차를 계산하는 함수이다.
보통 손실함수는 다음과 같이,
알고리즘이 출력한 \(y\)의 예측값인 \(\hat{y}\)과 참값 \(y\)의 제곱 오차의 반인 식을 사용한다.
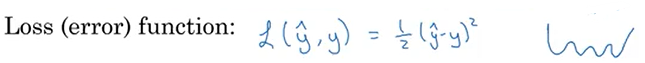
그러나, 로지스틱 회귀에서는 주로 사용하지 않는다.
> 매개 변수들을 학습하기 위해 풀어야할 최적화 함수가 블록하지 않아 여러 개의 지역 최소값에 빠질 수 있기 때문이다. 즉, 이럴 경우 경사 하강법이 전역 최적값을 못 찾을 수도 있다.
따라서, 로지스틱 회귀에서 사용하는 손실함수는 다음과 같다:

이 함수를 사용하는 직관적인 이유는 다음과 같이 두가지 경우로 나눌 수 있다.

- \(y=0\) 인 경우 \(L(\hat{y},y) = -log(1-\hat{y})\)가 0에 가까워지도록 \(\hat{y}\)는 0에 수렴하게 된다.
- \(y=1\) 인 경우 \(L(\hat{y},y) = -log(\hat{y})\)가 0에 가까워지도록 \(\hat{y}\)는 1에 수렴하게 된다.
하나의 입력에 대한 오차를 계산하는 함수를 손실 함수라고 하며, 모든 입력에 대한 오차를 계산하는 함수는 비용함수(cost function)라고 한다.
따라서, 비용함수는 모든 입력에 대해 계산한 손실 함수의 평균값으로 구할 수 있으면 다음과 같다.

항상 기억해야할 것은, 우리는 실제값과 비슷한 예측값을 원한다. 즉, 비용함수의 값이 작아지도록 하는 w와 b를 찾는 게 우리의 목표이다.
'Coursera 강의 > Deep Learning Specialization' 카테고리의 다른 글
- Total
- Today
- Yesterday
- computation graph
- numpy 배열 속성
- baekjoon
- Sort
- state value function
- Andrew Ng
- 강화학습
- 앤드류응
- sorted
- 백준
- 11870
- 강의노트 정리
- numpy 배열 생성
- omp: error #15
- **kwargs
- action value function
- 파이썬
- 로지스틱 회귀
- 경사하강법
- *args
- 비용함수
- NumPy
- python
- 숏코딩
- **
- 손실함수
- *
- adrew ng 머신러닝 강의
- 딥러닝
- policy function
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
