티스토리 뷰
[RL 강화학습] Markov Process, Markov Reward Process, Markov Decision Process 개념
Life4AI 2024. 7. 3. 20:10
강화학습은 순차적 의사결정 문제(sequential decision making)를 푸는 방법론이다. 문제를 잘 풀기 위해서는 문제를 잘 정의해야 한다. 따라서, 강화학습에서 문제를 정의할 때는 주어진 상황을 MDP (Markov Decision Process)의 형태로 변환해야 한다. MDP는 순차적 의사결정 문제를 수학적으로 정확하게 모델링하는 개념이다.
MDP에 대해 자세히 알아보기 전에, 간단히 MP (Markov Process)와 MRP (Markov Reward Process)에 대해 설명하겠다.
마르코프 성질 (markov property)
마르코프 성질은 확률 과정(stochastic process)의 특수한 형태로, memoryless하다. 이는 과거에 일어났던 일들과 무관하게 현재의 상태만이 미래의 상태에 영향을 미친다는 것을 의미한다.
이렇게 과거의 상태를 고려하지 않고 현재만을 고려하면 문제를 해결하기에 훨씬 수월해진다. 마르코프 성질을 조건부 확률로 나타내면 아래와 같다.

현재 상태 \(s_{t}\)만 알면 미래 상태 \(s_{t+1}\)를 예측하는 데 충분하다. 즉, 이전 상태들(\(s_{1},s_{2},...,s_{t-1}\))은 전혀 영향을 미치지 않는다.
agent가 environment에서 어떠한 action을 선택하기 위해서는 environment으로부터 정보들을 받게 되는데 이러한 정보들의 특성을 markov property라고 한다. 마르코프 성질을 가정함으로써, agent는 현재 시점에서 미래 가치를 예측하고 그에 따른 의사결정을 할 수 있게 된다.

현재 상태인 \(s\)와 연속된 다음 상태를 \(s'\)라고 했을 때 상태가 \(s\)에서 \(s'\)로 변경될 확률을 위와 같이 수학적으로 표현할 수 있다.
** 확률 과정(stochastic process)
시간의 흐름에 따라 확률적(random)으로 변화하는 상태를 나타낸다. (\({X_{t}}\)로, \(X\)는 radom variable, \(t\)는 시간)
>> 확률적이라는 것은 무작위성(randomness)을 의미한다
Markov Process (Markov Chain)
현재 상태에서만 미래 상태로의 전이 확률이 결정되는 무기억(random memoryless) 성질을 가지고 있다. 이는 현재 상태가 미래에 영향을 미치는 유일한 정보라는 뜻이다.
- 시간이 이산적일 때, Markov chain이라고 하며,
- 시간이 연속적일 때, Markov process라고 한다.

대학생들이 학교에서 수업에 참여하는 혹은 딴짓하는 예제이다.

MP의 주요 구성요소 \((S, P) \)
- 상태 집합 \(S\):가능한 상태들을 모두 모아놓은 집합
\(S=\{C1,C2,C3,Pass,Pub,FB,Sleep\}\)
- 전이 확률 행렬 \(P_{ss'}\): 상태 \(s\)에서 다음 상태 \(s'\)에 도착할 확률

다음은 예제 상황에서 몇가지 에피소드를 만들어보았다. 순서대로 상태가 변화하는 것을 볼 수 있다.

이때 sleep state를 terminal state라고 한다. 모든 프로세스가 종료되는 시점을 의미한다.
episode의 sampling
- 에피소드(episode) : 시작 상태 \(s_{0}\)에서 출발하여 종료 상태 \(s_{t}\)까지 가능한 여정
- 샘플링 (sampling): 매번 에피소드는 다를 수 있으며 각각의 과정이 샘플링
- 각 샘플링마다 리턴이 다를 수 있음
- 많은 경우 실제 확률 분포를 알기 어려우므로 샘플링을 통해 어떤 값을 유츄
Markov Reward Process
MRP는 Markov chain에다가 values라는 개념을 추가한 것이다. 이 가치를 판단하기 위해서는 두가지 factor인 reward와 discount factor가 추가된다.
(Markov Process는 state와 state transition만 주어지며, state transition이 얼마나 가치있는 지 알수 없음. MRP는 state transition의 가치까지 계산할 수 있음)

MRP의 주요 구성 요소 \((S, P, R, \gamma) \)
- 상태 집합 \(S\):가능한 상태들을 모두 모아놓은 집합
- 전이 확률 행렬 \(P_{ss'}\): 상태 s에서 다음 상태 S'에 도착할 확률
- 보상 함수 \(R\): 어떤 상태 s에 도착했을 때 받게 되는 보상
- 감쇠 인자 \(\gamma\): 0에서 1사이의 숫자
미래에 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길지를 나타내는 파라미터
학생 예제에 MRP를 적용해보자.

이전 예제와 달리, 빨간색의 reward가 추가된 것을 볼 수 있다.
- class 1 -> class 2: 50% 확률로 이동하며, 보상 -2 값을 받게 된다.
- class 3 -> pass -> sleep: 성공 후 보상 +10, 그 후 terminal state로 보상 0
강화학습에서 우리가 최종적으로 목표로 하는 것은 reward을 최대화하는 것이다. 이를 위해 우리는 감쇠된 보상의 합, 즉 리턴(return)을 계산한다. 리턴은 현재 시점에서 미래에 받을 모든 보상의 합을 할인율(discount factor) \(\gamma\)를 적용해 계산한다.
감쇠된 보상의 합, return
리턴 \(G_{t}\)는 \(t\)시점부터 미래에 받게 될 보상의 총합이다. 리턴값은 전체 환경이 아닌, 하나의 에피소드(경로)를 기준으로 계산되며, 이 리턴값을 통해 에피소드의 가치나 효율성을 평가할 수 있다.

즉, \(t\) 시점에서 앞으로 받게 될 미래의 보상들이 \(\gamma\)에 의해 할인되어 현재 가치로 환산된다. 이를 통해 강화학습은 보상을 단순히 최대로 하는 것이 아니라, 리턴을 최대화하도록 학습하게 된다.
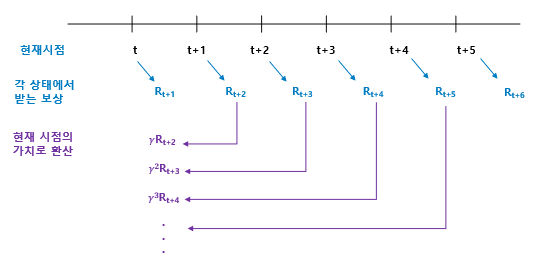
리턴값은 이미 정해진 하나의 경로(에피소드)에서 받는 보상을 계산하는 것이기 때문에 state transition probability를 고려하지 않는다. 즉, 이미 경로가 결정된 상태이므로, 상태전이확률을 적용할 필요가 없다.
학생예제에 각각의 에피소드들에 대한 value(return값)를 구해보면 다음과 같다.
가장 모범생의 행동 스타일이 가장 좋은 value 값을 가지고 있는 걸 볼 수 있다.

\(\gamma\)는 왜 필요하나? 역할이 무엇인가?
미래 보상을 현재의 가치로 환산할 때 사용되며, 0에서 1 사이의 값을 가진다.
- \(\gamma=0\): 미래의 보상은 모두 0으로 현재의 보상만 생각하는 탐욕적(greedy)인 보상
- : 여러 번 곱하면 0에 가까워짐, 현재의 보상이 100 스텝 후 받는 보상보다 훨씬 더 큰 값이 됨
- \(\gamma=1\): 현재의 보상과 미래의 보상이 동등, 장기적은 시야를 갖는 보상
> 수학적 편리성
\(\gamma\)를 1보다 작게 해줌으로써 return \(G_{t}\)가 무한의 값을 가지는 것을 방지, 즉 수렴하게 된다.
> 사람의 선호 반영
5년 후에 받는 100만원보다는 현재 받는 100만원을 선호한다.
> 미래에 대한 불확실성 반영
5년 후에 받을 100만원에 대한 미래의 가치의 불확실성을 반영한다.
MRP에서 각 상태의 Value 평가하기, value function
- 현재 상태 \(s_{t}\)의 value는 미래에 받을 보상의 기대값이며, value function을 통해 state의 value를 평가하고, 이 가치를 최대화하는 방향으로 학습이 진행된다.
- value function: 현재 상태 \(s_{t}\)에서 시작하여 리턴 \(G_{t}\)의 기댓값(expectation)을 계산한다.
- 이를 통해 에이전트는 각 상태에서 장기적인 보상을 최대화할 수 있는 방향으로 학습할 수 있다.

이러한 value function을 Bellman Equation을 통해서 현재 보상과 다음 상태에서의 가치로 표현할 수 있는 것을 알 수 있다. 이건 다음 포스팅에서 자세하게 설명하겠다.
학생예제에 state-value function을 계산해보자.

상태가침함수는 환경 전체에 대한 가치를 측정하며, 리턴값은 에피소드 하나에 대한 가치를 측정한다. 또한, 상태전이확률을 고려한다는 점이 리턴값과 다른 점이다.
| 측정 대상 | 특징 | discount factor \(\gamma\) | 상태전이확률 \(P\) | |
| return G | 에피소드 | 합계 | 사용 | 미사용 |
| state-value function V | 전체 환경 | 기대값 | 사용 | 사용 |
Markov Decision Process
MRP에 순차적 의사결정의 핵심인 decision에 대한 개념을 추가한 것이다.

MDP의 주요 구성 요소 \((S, A, P, R, \gamma) \)
- 상태 집합 \(S\):가능한 상태들을 모두 모아놓은 집합
- 액션 집합 \(A\): 에이전트가 취할 수 있는 행동들을 모아놓은 집합
- 전이 확률 행렬 \(P_{ss'}\): 상태 s에서 다음 상태 S'에 도착할 확률
> MP, MRP: 현재 상태 \(s\)일 때 다음 상태 \(s'\)가 될 확률: \(P_{ss'}\)
> MDP: 현재 상태 \(s\)일 때 에이전트가 액션 \(a\) 선택했을 때 다음 상태 \(s'\)가 될 확률: \(P_{ss'}^{a}\)
- 보상 함수 \(R_{s}^{a}\): 상태 s에서 액션 \(a\)를 선택하면 받는 보상함수
- 감쇠 인자 \(\gamma\): 0에서 1사이의 숫자
미래에 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터
학생 예제에 MDP를 적용해보면, class 1의 state에서 할 수 있는 action은 study, facebook이 될것이다.
만약 study라는 action을 취하면 reward는 -2를 얻고 다음 state인 class 2로 이동한다.

행동의 정책, \(\pi\)
정책(policy)는 agent가 행동을 하는데 중요한 역할로, 현재 상태에서 모든 행동들에 대한 확률 분포이다.
이를 현재 state와 action을 mapping한다라고도 표현한다.

상태는 markov 성질을 가지므로, 현재 상태만으로도 행동을 의사결정할 수 있다. 즉, 현재 상태만으로 action을 stochastic하게 결정하게 된다.
그리고 policy는 time step의 변화에 무관하게 독립적으로 진행이 되므로 stationary하다고 할 수 있다. 이는 시간이 지남에 따라 agent가 동일한 상태를 여러번 지나간다 해도 그 상태에 있을 때의 행동 전략은 변하지 않는다는 의미이다.
정책을 고려한 상태전이행렬과 보상함수는 다음과 같다.

'AI > 강화학습 (Reinforcement Learning)' 카테고리의 다른 글
| [RL 강화학습] 정책과 2가지 가치 함수: Policy, Value function (0) | 2024.10.02 |
|---|---|
| [RL 강화학습] 강화학습이란? (0) | 2024.05.20 |
- Total
- Today
- Yesterday
- 11870
- omp: error #15
- 로지스틱 회귀
- 손실함수
- **kwargs
- computation graph
- *
- **
- numpy 배열 속성
- *args
- 백준
- Sort
- 앤드류응
- 비용함수
- sorted
- python
- 강화학습
- state value function
- adrew ng 머신러닝 강의
- 숏코딩
- NumPy
- action value function
- numpy 배열 생성
- 딥러닝
- policy function
- 파이썬
- baekjoon
- 경사하강법
- Andrew Ng
- 강의노트 정리
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
